I’ve previously written about how impedance reveals the fabric of the universe. I’ve also written about how PA systems are enormous, tuned circuits implemented in the acoustic domain.

What I haven’t really gotten into is the whole concept of finite versus infinite impulse response. This follows along with the whole “resonant circuit” thing. A resonant circuit useful for audio incorporates some kind of feedback into its design, whether that design is intentional (an equalizer) or accidental (a PA system). Any PA system that amplifies the signals from microphones through loudspeakers which are audible to those same microphones is an IIR filter. That re-entrant sound is the feedback, even if the end result isn’t “feedback” in the traditional, loud, and annoying sense. Even if the PA system uses FIR filters for certain processing needs, the device as a whole exhibits infinite impulse response when viewed mathematically.

What the heck am I talking about?

FIR, IIR

Let’s first consider the key adjectives in the terms we’re using: “Finite” is one, and “infinite” is the other. The meanings aren’t complicated. Something that’s finite has an endpoint, and something that’s infinite does not. The infinite thingamabob just goes on forever.

The next bit to look at is the common subject that our adjectives are modifying. The impulse response of a PA system is what output the system produces when an input signal is applied.

So, if you stick both concepts together, a finite impulse response would mean that the PA system output relative to the input comes to a stop at some point. An infinite impulse response implies that our big stack of sound gear never comes to a stop relative to the input.

At this point, you’re probably thinking that I’ve got myself completely backwards. Isn’t a PA an FIR device? If we don’t have “classic” feedback, doesn’t the system come to a stop after a signal is removed? Well, no – not in the mathematical sense.

Functionally FIR, Mathematically IIR

First, let me talk about a clear exception. It’s entirely possible to use an assemblage of gear that’s recognizable as a PA system in a “playback only” context. The system is used to deliver sound to an audience, but there are no microphones involved in the realtime activity. They’re all muted, or not even present. Plug in any sort of signal source that is essentially impervious to sound pressure waves under normal operation, like a digital media player, and yes: You have a system that exhibits finite impulse response. The signal exiting the loudspeakers is never reintroduced to an input, so there’s no feedback. When the signal stops, the system (if you subtract the inherent, electronic noise floor) settles to a zero point.

But let’s look at some raw math when microphones are involved.

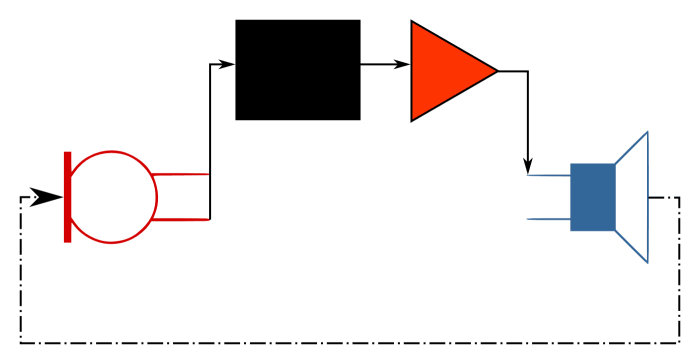
An acoustical signal is presented to a microphone capsule. The microphone converts the acoustical signal to an electrical one, and that electrical signal is then passed on to a whole stack of electronic doodads. The resulting electrical output is handed off to a loudspeaker, and the loudspeaker proceeds to convert the electrical signal into an acoustical signal. Some portion of that acoustical signal is presented to the same microphone capsule.

There’s our feedback loop, right?

Now, in a system that’s been tuned so as to behave itself, the effective gain on a signal traveling through the loop is a multiplier of less than one. (Converted into decibels, that means a gain of less than 0 dB.) Let’s say that the effective gain on the apparent pressure – NOT power – of a signal traversing our loop is 0.3. This means that our microphone “hears” the signal exiting the PA at a level that’s a bit more than 10 dB down from what originally entered the capsule.

If we start with an input sound having an apparent pressure of “1”:

And so on.

In a mathematical sense, the PA system NEVER STOPS RINGING. (Well, until we hit the appropriate mute button or shut off the power.) The apparent pressure never reaches zero, although it gets very close to zero as time goes on.

And again, this brings us back to the concept of our rig being functionally FIR, even though it’s actually IIR. It is entirely true that, at some point, the decaying signal becomes completely swallowed up in both the acoustical and electrical noise floors. After a number of rounds through the loop, the signal would not be large enough to meaningfully drive an output transducer. As far as humans are concerned, the timescale required for our IIR system to SEEM like an FIR system is small.

Fair enough – but don’t lose your sense of wonder.

Fractal Geometries and Application

Although the behavior of a live-audio rig might not quite fit the strict definition of what mathematicians call an iterated function system, I would argue that – intriguingly – a PA system’s IIR behavior is fractal in nature. The number of loop traversals is infinite, although we may not be able to perceive those traversals after a certain number of iterations. Each traversal of the loop transforms the input in a way which is ultimately self-similar to all previous loop inputs. A large peak may develop in the frequency response, but that peak is a predictable derivation of the original signal, based on the transfer function of the loop. Further, in a sound system that has been set up to be useful, the overall result is “contractive:” The signal’s deviation from silence becomes smaller and smaller, and thus the signal peaks come closer and closer together.

I really do think that the impulse behavior of a concert rig might not be so different from a fractal picture like this:

And at the risk of an abrupt stop, I think there’s a practical idea we can derive from this whole discussion.

A system may be IIR in nature, but appear to be FIR after a certain time under normal operating conditions. If so, the transition time to the apparent FIR endpoint should be small enough that the system “ring time” does not perceptibly add to the acoustical environment’s reverb time.

Think about it.