Tag Archives: Amplifiers

The Pro-Audio Guide For People Who Know Nothing About Pro-Audio, Part 7

Amplifiers and loudspeakers bring us to the end of my series for Schwilly Family Musicians.

Please Remember:

The opinions expressed are mine only. These opinions do not necessarily reflect anybody else’s opinions. I do not own, operate, manage, or represent any band, venue, or company that I talk about, unless explicitly noted.

Want to use this image for something else? Great! Click it for the link to a high-res or resolution-independent version.

“Now that we’ve turned audio into electricity and back again, we’ve reached the end of this series.”

This article is available, for free, right here.


Drivers Don’t Have To Die With A Bang

Sane powering shields you from accidents.

Please Remember:

The opinions expressed are mine only. These opinions do not necessarily reflect anybody else’s opinions. I do not own, operate, manage, or represent any band, venue, or company that I talk about, unless explicitly noted.

Want to use this image for something else? Great! Click it for the link to a high-res or resolution-independent version.

I once lived in abject terror of pops, clicks, and bangs. I was once frightened by the thought of a musician unplugging their instrument from a “hot” input before I found the mute button. This was a result of my early experience in audio, where well-meaning (but incorrect) people had assured me that such noises were devastating to loudspeakers. A good solid “thump” from powering up a console when the amps were already on, and some poor driver would either:

A) Take another step towards doom, or…

B) Blow up like that one space station that could be confused with a small moon.

Well, that’s just a load of horsefeathers, but like all audio myths, a kernel of truth can be found. The kernel of truth is that loudspeakers CAN be destroyed by a large spike of input. There’s a reason that drivers and loudspeaker enclosures have peak ratings. Those are “Do Not Exceed” lines that you are smart to avoid crossing. Here’s the deal, though – if you’re using a sane powering strategy with passive boxes, or are using any truly decent powered speaker, worry is essentially unnecessary.

An amplifier simply can not “swing” more voltage than is available from the supply. If the peak voltage available from the amp results in power dissipation equal to or less than what the loudspeaker can handle, a brief transient won’t cook your gear. The instantaneous maximum power will be in the safe range, and the whole signal won’t last long enough for the continuous power to become a factor. An active box that’s well designed will either be powered in such a way, or it may be overpowered and then limited back into a safe range.

So, when a system is set up correctly, the odd mishap isn’t necessarily dangerous. It’s just displeasing to hear.

I believe that the persistence of this myth is due to folks who get talked into “squeezing maximum performance” out of their loudspeakers. They’re told that they have to use very large amplifiers to drive the boxes they have, and so that’s what they do. They hook up amps that can handily deliver power far beyond the “Do Not Exceed” line specified by peak ratings. If they take no other safety precautions, they ARE playing with fire. One good, solid accident, and that may be it for a driver. (If I might be so bold, I would recommend that those folks instead use my speaker powering strategy instead of “spend lots more, maybe get a touch louder, and hope you’re lucky.”)

The worrier doesn’t have to be you. Keep things reasonable, and you’ll be very unlikely to lose money because somebody yanked a cable.


How Much Output Should I Expect?

A calculator for figuring out how much SPL a reasonably-powered rig can develop.

Please Remember:

The opinions expressed are mine only. These opinions do not necessarily reflect anybody else’s opinions. I do not own, operate, manage, or represent any band, venue, or company that I talk about, unless explicitly noted.

howloudWant to use this image for something else? Great! Click it for the link to a high-res or resolution-independent version.

As a follow-on to my article about buying amplifiers, I thought it would be helpful to supply an extra tool. The purpose of this calculator is to give you an idea of the SPL delivered by a “sanely” powered audio rig.

A common mistake made when estimating output is to assume that the continuous power the amp is rated for will be easily applied to a loudspeaker. This leads to inflated estimations of PA performance, because, in reality, actually applying the rated continuous power of the amp is relatively difficult. It’s possible with a signal of narrow bandwidth and narrow dynamic range – like feedback, or sine-wave synth sounds, but most music doesn’t behave that way. Most of the time, the signal peaks are far above the continuous level…

…and, to be brutally honest, continuous output is what really counts.

This Calculator Requires Javascript

This calculator is an “aid” only. You should not rely upon it solely, especially if you are using it to help make decisions that have legal implications or involve large amounts of money. (I’ve checked it for glaring errors, but other bugs may remain.) The calculator assumes that you have the knowledge necessary to connect loudspeakers to amplifiers in such a way that the recommended power is applied.

Enter the sensitivity (SPL @ 1 watt @ 1 meter) of the loudspeakers you wish to use:

Enter the peak power rating of your speakers, if you want slightly higher performance at the expense of some safety. If you prefer greater safety, enter half the peak rating:

Enter the number of loudspeakers you intend to use:

Enter the distance from the loudspeakers to where you will be listening. Indicate whether the measurement is in feet or meters. (Measurements working out to be less than 1 meter will be clamped to 1 meter.)

Click the button to process the above information:

Recommended amplifier continuous power rating at loudspeaker impedance:
0 Watts

Calculated actual continuous power easily deliverable to each loudspeaker:
0 Watts

Calculated maximum continuous output for one loudspeaker at 1 meter:
0 dB SPL

Calculated maximum continuous output for one loudspeaker at the given listening position:
0 dB SPL

Calculated maximum continous output for entire system at the given listening position:
0 dB SPL

How The Calculator Works

First, if you want to examine the calculator’s code, you can get it here: Maxoutput.js

This calculator is intentionally designed to give a “lowball” estimate of your total output.

First, the calculator divides your given amplifier rating in half, operating on the assumption that an amp rated with sine-wave input will have a continuous power of roughly half its peak capability. An amp driven into distortion or limiting will have a higher continuous output capability, although the peak output will remain fixed.

The calculator then assumes that it will only be easy for you to drive the amp to a continuous output of -12 dB referenced to the peak output. Driving the amp into distortion or limiting, or driving the amp with heavily compressed material can cause the achievable continuous output to rise.

The calculator takes the above two assumptions and figures the continuous acoustic output of one loudspeaker with a continuous input of -12 dB referenced to the peak wattage available.

The next step is to figure the apparent level drop due to distance. The calculator uses the “worst case scenario” of inverse square, or 6 dB of SPL lost for every doubling of distance. This essentially presumes that the system is being run in an anechoic environment, where sound pressure waves traveling away from the listener are lost forever. This is rarely true, especially indoors, but it’s better to return a more conservative answer than an “overhyped” number.

The final bit is to sum the SPLs of all the loudspeakers specified to be in the system. This is tricky, because the exact deployment of the rig has a large effect – and the calculator can’t know what you’re going to do. The assumption is that all the loudspeakers are audible to the listener, but that half of them appear to be half as loud.


A Tiny Bit Of Practical Math For Audio Folks

If a number is part of a nonlinear operation, the only way to extract that number is through a nonlinear operation.

Please Remember:

The opinions expressed are mine only. These opinions do not necessarily reflect anybody else’s opinions. I do not own, operate, manage, or represent any band, venue, or company that I talk about, unless explicitly noted.

logcurveWant to use this image for something else? Great! (No high-res on this one. Sorry – I forgot.)
I personally think it’s very handy for audio humans to be able to look at concepts quantitatively. That is, with measurements. It’s a great way to suss out what’s really happening with an audio rig.

Quite often, when trying to work with audio issues involving math, you end up with an unknown in an “inconvenient” place. Finding the unknown means some algebraic acrobatics – which wouldn’t be a big deal if not for the mathematics of sound being funky.

Audio math isn’t just bog-simple linear operations. It’s also nonlinear in nature, and the nonlinear bits (that is, logarithms) can make the algebra confusing. It’s confusing to the point that folks like me, who’ve been involved with audio for a good long while, can still go about something in entirely the wrong way.

But there’s one thing I finally realized. It’s one of those things that was probably explained to me ages ago, but didn’t “take” for some reason. It’s a realization that makes things much easier:

For the purposes of algebra, a logarithm encapsulates the connected number or expression that REPRESENTS a number. You can NOT extract the connected number or expression through linear means.

If you just said, “What?” then don’t worry. I can give you an example.

Let’s say that you’ve got an amplifier that can output a momentary, undistorted peak of 500 watts into a loudspeaker connected to one of the channels. What you’re curious about is a ballpark figure regarding the continuous power involved when you reach that peak. You figure that the crest factor of the signals sent to the amp (the ratio of peak to RMS voltage) is about 12 dB. Remembering your basic audio math, you work this up:

10 log10 x/500 = -12 dB

In other words, an unknown number of watts compared to the known peak power of 500 watts is -12 dB. (The decibel in this case is being referenced to 500 watts.)

Dividing both sides of the equation by 10 is appropriate, because that “10” on the left is engaged in the linear operation of multiplication. As such, the linear operation of division is the inverse. You end up with:

log10 x/500 = -1.2 dB

Now – it’s very tempting to try a linear operation to “move x” to a convenient spot. You might think that dividing by x gets you this (which becomes easy to work out on a calculator):

log10 1/500 = -1.2 dB/x
-2.6989 = -1.2 dB/x
-2.6989x = -1.2 dB
x = -0.444 watts

Nope. That can’t be right. For a start, there’s no such thing as negative power. For another, 10 dB down from 500 watts is 50 watts, and 3 dB down from that is 25 watts, so the number -0.444 isn’t even close. Even if you didn’t know that, plugging -0.444 into the original equation yields an answer that doesn’t agree with the original conditions:

10 log10 -0.444/500 = -12 dB
log10 -0.444/500 = -1.2 dB
[Calculator Returns: Invalid Input] ≠ -1.2 dB

Remember what I said: The logarithm is encapsulating the “x/500.” That is to say, x/500 is NOT two numbers in this case. It’s one number, represented by an expression, and we’re trying to take the logarithm of it. The only way to get the number “x/500” out into a place where you can use linear math is to reverse the logarithm. Here’s where we were before things went wrong:

log10 x/500 = -1.2 dB

The inverse of a logarithm is an exponent. The logarithm’s base is nothing more exotic than the base number that the exponent raises, and the exponent itself is whatever is on the other side of the equation.

10^-1.2 = x/500

NOW you can use linear math.

0.0630 = x/500
31.548 = x

Put that back into the original equation, and things work out perfectly.

10 log10 31.548/500 = -12 dB
log10 31.548/500 = -1.2 dB
log10 0.0630 = -1.2 dB
-1.2 dB = -1.2 dB

So, if you remember that extracting numbers from nonlinear operations requires an inverse nonlinear operation, you’ll figure out that the continuous power across your speakers is about 31 watts.

(Incidentally, this is one of the reasons why big PA systems are so big, but that’s a discussion for another day…)


Holistic Headroom

If you have zero headroom anywhere, you have zero headroom everywhere.

Please Remember:

The opinions expressed are mine only. These opinions do not necessarily reflect anybody else’s opinions. I do not own, operate, manage, or represent any band, venue, or company that I talk about, unless explicitly noted.

“Headroom” is a beloved buzzword for audio craftspersons. Part of the reason it’s beloved is because you can blame your problems on the lack of it:

“I hate those mic pres. They don’t have enough headroom.”

“I’m always running out of headroom on that console’s mix buses.”

“I need to buy a more powerful amplifier for my subs, because I this one doesn’t have enough headroom.”

(I’m kinda tipping my hand a bit with that last one, in terms of this post being sort of a “follow on” to my article about clipping.)

Headroom is sometimes treated as a nebulous sort of concept – a hazy property that really good gear has enough of, and not-so-good gear doesn’t possess in the required quantity. In my opinion, though, headroom is pretty easy to define, and its seeming mysteriousness is due to it being used as a “blamecatcher” for things that didn’t go as planned.

Headroom, as I was taught, is “the difference between the maximum attainable level and the nominal level.” In other words, if a device can pass a signal of greater intensity than is required for a certain situation, then the device has some non-zero amount of headroom. For example, if your application requires a console’s main bus to pass 0 dBu (decibels referenced to 0.775 volts, RMS), and the console can pass +24 dBu, then you have 24 dB of headroom in the console.

(If it’s available, and ya ain’t usin’ it, it’s headroom.)

The overall concept is pretty easy to understand, but what a good number of folks aren’t taught, and often fail to realize for a good long while (this includes me), is that headroom is holistic, and “lowest common denominator.” That is to say:

Two or more audio components – whether electrical or acoustical – connected together all have the SAME effective headroom, and that effective headroom is equal to the LOWEST amount of headroom available at any point in the signal chain.

So…what the heck does that mean?

Everything Has A Maximum Level – Everything

To start with, it’s important to point out that hyphenated bit in the above definition. Especially because this is a site about live-performance, what you have to realize is that absolutely everything connected to that live performance has a maximum amount of appropriate signal intensity. Even acoustical sources and your audience qualify for this. Think about it:

A singer can’t sing any louder than they can sing.

A mic can only handle so much SPL.

A preamp can only swing a limited amount of voltage at its outputs.

Different parts of a console’s internal signal path have limits on how much signal they can handle.

A power amplifier can’t deliver an infinite amount of voltage.

Speakers handle a limited amount of power.

The people listening to the show have a finite tolerance for sound pressure.

…and every single one of these “components” is connected to the others. Sure, the connection may not be a direct, electrical hookup, but the influences of other parts of the system are still felt. If your system can create a “full tilt boogie” sound pressure level of 125 dB SPL C, but your audience will only tolerate about 105, then that lower level becomes your “don’t exceed” point. Go beyond it, and you effectively “clip” the audience…which makes your 20 dB of unused PA capability partially irrelevant. That leads to my next point.

Your Minimum Actual Headroom Is All You Effectively Have

Sometimes, a singer will “run out of gas.” They may have strained themselves, or they might not be feeling well, or they might just be tired. As a result, their maximum acoustical output drops by some amount.

Here’s the thing.

The entire system’s EFFECTIVE headroom has just dropped by that amount. If the singer is 10 dB quieter than they used to be, you’ve just lost 10 dB of effective headroom.

Now – before you start getting bent out of shape, complaining that your console’s mix bus headroom hasn’t magically changed, look at that paragraph again. The key is the word “effective.”

Of course your console can still pass its maximum signal. Of course your loudspeakers still handle the same power as they did a moment ago. As isolated components, their absolute headroom has not changed in any way.

But components working in a complete electro-acoustical system are not isolated, and are therefore limited by each other in various ways.

In the case of a singer getting worn out, their vocal “signal” drops closer to the noisefloor of the band playing around them. Now, if we were talking about an electrical device, the noisefloor staying the same with a decrease in maximum level above that noisefloor would be – what? Yes: A loss of headroom.

The way this affects everything else is that you now have to drive the vocal harder to get a similar mix. (It’s not the same mix, because there’s less acoustical separation between the singer and the band at the point of the mic capsule, but that’s a different discussion.) Because the singer’s overall level has dropped, your gain change might not be pushing you any closer to clipping an electrical device…but you are definitely closer to the point where your system will “ring” with feedback. A system in feedback, effectively, has reached its maximum available output.

Your effective headroom has dropped.

A Bigger Power Amp Isn’t Enough

Okay – here’s the bit that’s directly related to my “clipping” article.

The concept of holistic headroom is one of the larger and fiercer bugaboos to be found in the piecing together of live-audio rigs. As many bugaboos do, it grows to a fearsome size by feeding on misconceptions and mythology. There is a particular sub-species of this creature that’s both common and venomous: The idea that a system headroom problem can be fixed by purchasing more powerful amplifiers.

Now, if you’re constantly clipping your amps because the system won’t get loud enough for your application, then yes, you need to do something about the problem. However, what you need to do has to be effective on the whole, and not just for one isolated part of the signal chain. Buying a bigger amplifier will probably get you some headroom at the amplifier, but it might not actually get you any more effective headroom (which is what actually matters). If your old amplifier’s maximum level was equal to your speakers’ power handling, and the new amplifier is more powerful than the old one, then you’ve done nothing in terms of effective headroom.

The loudspeakers were already hitting their maximum level. As such, they had zero headroom, and your new amp is thus effectively limited to zero additional headroom. Your enormously powerful amp is doing virtually nothing for you, except for letting you hit your unchanged maximum level without seeing clip lights.

To be fair, the system will get somewhat louder because loudspeakers don’t “brickwall” at their maximum input levels. Also, the nature of most music is that the peaks are significantly higher than the continuous level, which lets you get away with a too-big amp for a while. You will get some more level for a while, but your speakers will die much sooner than they should – and when they do, your system will become rather quieter…

Anyway.

The point is that, if you want a system headroom increase of “x” decibels, then you have to be sure that every part of your system – not just one piece – has “x” more decibels to give you. If you’re going to get more power, you have to make sure that you also have that much more “speaker” to receive that power. (And this gets into all kinds of funny business, like whether or not you can buy speakers that are just as efficient as what you’ve had while handling more power, or whether you need to buy more of the same speakers, and if that’s a good idea because of arrayability, or…)

There’s also the question of whether or not a more powerful system is what your audience even wants. It all ties together, because headroom is holistic.


Clipping Does NOT Kill Loudspeakers

Clipping can be associated with a loudspeaker being cooked, but it isn’t really the cause.

Please Remember:

The opinions expressed are mine only. These opinions do not necessarily reflect anybody else’s opinions. I do not own, operate, manage, or represent any band, venue, or company that I talk about, unless explicitly noted.

It’s very likely that – if you’ve ever been involved in live-sound – you’ve heard something like this: “You have to use very powerful amps on your speakers, because clipping will blow the drivers.”

This idea is one of the most long-standing live-sound myths in existence. Its ability to stubbornly persist as an accepted notion is remarkable, although not astounding. That is, it’s not surprising that the myth survives, because it’s backed up by observations made by intelligent people.

The problem is that the observations are being interpreted incorrectly. If you want to “have the right of it,” then you need to remember this:

Clipping is not a cause of speaker failure. It can occur alongside conditions that cause speaker failure, and it can precipitate conditions that cause speaker failure, but it is not actually dangerous in itself.

Okay. Fine. Where’s any support that what I just said is correct?

Well, to start with…

Thousands Of Guitar Amps Are – Miraculously – Still Alive

How many guitar players do you know that have to regularly replace the speakers in their rigs, because those speakers are constantly getting cooked? I don’t know any.

How many guitar players do you know who’s tone includes “crunch,” or “drive,” or “fuzz,” or “distortion,” or who love it when the amp “breaks up” or “saturates?” The number is probably close to “all of them.”

Okay.

Distortion/ fuzz/ overdrive/ breakup/ whatever are ALL clipping. All of them. 100%. Some of them are clipping that happens in a circuit in front of the amp, which then gets passed through the amplifier “cleanly” (or not). Some of the most adored and sought-after sounds are the result of clipping the actual power-amp section – the bit that turns the signal into something with sufficient voltage and current to move loudspeakers around.

“Oh, but Danny, a distorted guitar amp is different from a distorted PA.”

Nope. Not in a fundamental sense.

Now, sure, an actually-clipping solid-state power amplifier may generate a different distribution of harmonics than an actually-clipping tube driven guitar amplifier, but the same thing is going on. A clipped signal is being pushed across loudspeaker drivers. Amazingly, the guitar amp’s speakers aren’t dying. Why?

Because the power they’re receiving is within their design limits. The distortion involved is barely relevant.

The Problem Is Too Much Power

What I’ve come to understand over the years is that, assuming everything else is copacetic, loudspeakers are only killed by amplifiers that supply too much power. It might be too much power for too long, or it might be too much power for a short time…at a low frequency.

That’s it.

So, if all kinds of guitar amplifiers aren’t killing their speakers, and if the problem is too much power, why does the myth persist? Why do people insist on mating big amplifiers to speakers, with the assumption that “headroom” will prevent drivers from meeting an untimely end? It’s pretty simple, actually – people tend to associate correlation with causation, even when the association is wrong.

Classic examples of this are found in human history. Something bad happens to a group of people at around the same time of a lunar eclipse, or when a comet is visible in the sky, and they start assuming that the cosmological event is the cause of their problem. In the same way, enough speakers have been wrecked while a clip light was illuminated to make people think that clipping was what wrecked their drivers.

…and so, they start to believe that running a really powerful amp without clipping is safer than running a less-powerful amp into clipping. It isn’t. Their original problem was that their “too small” amplifier can actually deliver a lot more power than they expect.

Amps Are More Powerful Than You Think. For An Instant.

Let’s say that we’ve just bought an amplifier, and we’re doing what we should be doing: We’re reading the manual. We get to the end, where the specifications live. The manufacturer says that the amp can deliver 400 watts per channel, continuous, at some impressively small distortion factor (like 0.02%), into an 8 ohm load.

Why is all that qualification necessary? It’s a 400 watt amplifier, right?

Not really.

As I’ve come to understand them, amplifiers are devices that put voltage across an attached device. You know – a speaker. Because they put voltage across the speaker, current flows. Because voltage and current are flowing, the circuit has an attendant amount of power being dissipated by the speaker – the power is converted to heat and sound.

The thing is, the voltage coming out of the amplifier is NOT constant. It’s not direct current…it can’t be. Direct current doesn’t change over time, so it can’t represent a sonic event. A sonic event changes over time by nature. No, the signal coming out of the amplifier is time variant. It’s alternating current, rather similar to what comes out of a “mains power” wall socket in a building. the primary differences are that the voltage coming out of the amplifier is significantly lower, and that we expect the signal from the amplifier to have a lot of frequencies present at similar voltages.

Music, in other words.

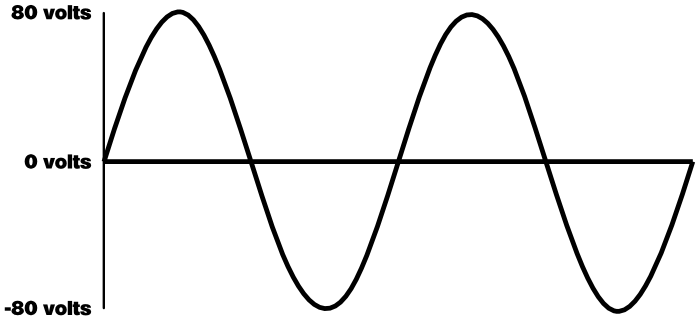
This creates a bit of a bugaboo. If the voltage from the amplifier varies as time passes, then the power delivered to the loudspeaker also varies as time passes. If we hook up a sine-wave generator to the amp, and then graph the amp’s output, we would get something like this:

There’s something very curious here. At the instant that the voltage is 0, no power is being presented to the loudspeaker. At that moment, we have a 0 watt amplifier. No voltage means no current, which means no power. Of course, at the very next instant the voltage is some non-zero value, which means that the power across the speaker is also non-zero.

What’s also curious – and key to this whole article – is what happens at the signal peaks. You’ll notice that they occur at 80 volts. If power is v^2/r (the square of voltage over the load resistance), then, for an instant, the amplifier delivers 800 watts to the speaker.

But it’s a 400 watt amp! What gives?

Remember all that “qualification” that was attached to that 400-watt number? It’s all required because the amp spends most of its time delivering more or less than 400 watts to our 8 ohm loudspeaker. The 400 watt figure is an average meant to convey what the amplifier can meaningfully do over the course of time, ultimately in terms of heat and sound produced by the speaker. For audio, we tend to find that values derived from RMS (Root Mean Square) voltages track well with how humans hear, so it’s very likely that the “continuous power” rating on our amp is the energy delivered from the RMS voltage that we can swing from the outputs.

For an amp that has a peak output voltage of +/- 80 volts, the sine-wave RMS voltage is about 56.57 volts. Using v^2/r, that comes out to 400 watts. If the loudspeaker is rated for 400 watts of continuous power, then we’re fine.

As long as we don’t push the amplifier too hard.

Not because of clipping, but because our amp is more powerful than we realize.

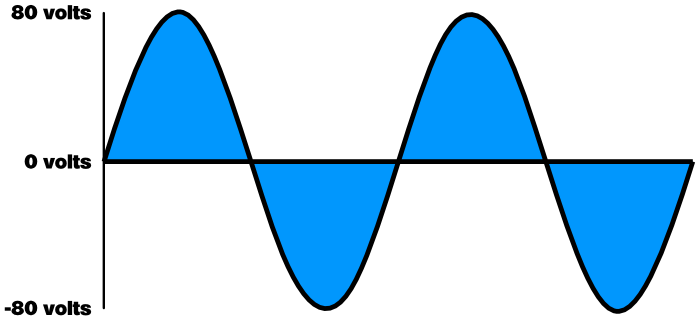
The Area Under The Curve

Here’s our diagram again. We’ve got ourselves a nice, undistorted signal. To help visualize the power being delivered to the loudspeaker, I’m going to fill in the “area under the curve,” or the space between 0 voltage and the amp’s output.

So, what happens if we push the amp beyond what it can do with inaudible distortion? Well, the amp can’t give us more voltage than it’s built to create, but it can give us the maximum voltage for a longer time. It might be able to do this “nicely,” by using internal dynamics processing to prevent the signal from actually generating a lot of nasty harmonics, or the amp might get into actual, unpleasant, super-saturated harmonic distortion overdrive. In either case, the output signal peaks flatten – and as they do, the continuous power delivered to the speaker gets closer and closer to the maximum power available from the amplifier. If I overlay the most extreme case of this over our original sine-wave, you can “see” the problem:

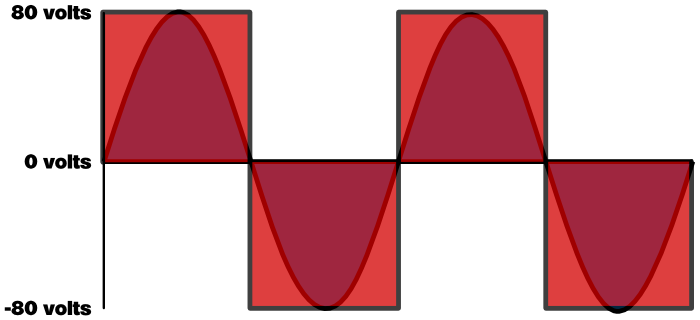
The closer you get to driving the amp into square-wave territory, the more that the RMS voltage and the peak voltage become the same thing. Assuming that the amp doesn’t go into thermal shutdown or engage other protection, you can deliver a LOT of continuous power into your loudspeaker. In terms of the example I’ve been using so far, you could be putting up to TWICE the loudspeaker’s rated power into the poor thing.

Do that for long enough, and the voice coil (or even something else) will overheat and fail. You’re left with smoke and silence.

Picking Up The Pieces

As you can see, the problem really isn’t clipping. Sure, clipping was involved in the process of wrecking the example loudspeaker, because it’s what had to happen for us to push our fictional amp into “too much power” territory.

What if we’d have used a bigger amp, though?

Here’s where things get into human psychology.

If we were willing to push a small amp into audible clipping (or even just limiting) for long enough to kill a loudspeaker, why would we think that we wouldn’t push a larger amp just as hard – if not harder? The big amp’s signal will stay nice and clean for much longer, and we might not be able to recognize the sounds of the drivers being beaten up. That being the case, we push our much larger amp well into the same overall power output, and our drivers start to get cooked again. Of course, we don’t see any clip lights, so we feel safe. The loudspeakers don’t die right away, because overpowering is rarely an “instant death” event, but they will die eventually. We didn’t see those evil little clip lights, though, so we assume that it’s just “wear and tear” or “defective drivers,” or “cheap gear.”

…but it was the same thing all along. Too much power.

Too much power is still the operative problem, even when true clipping at the amp hits a passive crossover and dumps extra energy into a high-frequency driver. Sure, if the amp hadn’t clipped, then that extra power wouldn’t have been present…but why were you running the rig so hard (and with such overpowered amps) that the power generated from the harmonics in a clipped signal could liquefy the HF driver’s voice coil? How could you stand to even listen to that? A smaller amp, clipped to the same degree, wouldn’t have killed the driver, although it would still have sounded terrible.

“Underpowering” isn’t the problem. Clipping isn’t the problem. Too much power and too much human error are the problem.