There’s a lot of math behind the sound of a show, but you don’t have to work it out symbolically.
Please Remember:
The opinions expressed are mine only. These opinions do not necessarily reflect anybody else’s opinions. I do not own, operate, manage, or represent any band, venue, or company that I talk about, unless explicitly noted.

 Want to use this image for something else? Great! Click it for the link to a high-res or resolution-independent version.
Want to use this image for something else? Great! Click it for the link to a high-res or resolution-independent version.This post is the fault of my high-school education, my dad, and Neil deGrasse Tyson.
In high-school, I was introduced to calculus. I wasn’t particularly interested in the drills and hairy algebra, but I did have an interest in the high-level concepts. I’ve kept my textbook around, and I will sometimes open it up and skim it.
My dad is a lover of cars, and that means he gets magazines about cars and car culture. Every so often, I’ll run across one and see what’s in the pages.
About a month ago, I was on another jaunt through my calculus book when I happened upon a car-mag with an article by Neil deGrasse Tyson. (You know Dr. Tyson. He’s the African-American superstar astrophysicist guy. He hosted and narrated the new version of “Cosmos.”) In that article was a one-line concept that very suddenly connected some dots in my head: Dr. Tyson pointed out that sustained speed isn’t all that exciting – rather, acceleration is where the fun is.
Acceleration.
Change.
The rate of change.
Derivative calculus.
Exciting derivative calculus makes for exciting music.
What?
Let me explain.
Δy/Δx: It’s Where The Fun Is!
The first thing to say here is that there’s no need to be frightened of those symbols in the section heading. The point of all this is not to say that everybody should reduce music to a set of equations. I’m not suggesting that folks should have to “solve” music in a symbolic way, as a math problem. What I am saying is that mathematical concepts of motion and change can be SUPER informative about the sound of a show. (Or a recording, too.)
I mean, gosh, motion and change. That sounds like it’s really important for an art form involving sine waves. And vibrating stuff, like guitar strings and loudspeakers and such.
Anyway.
Those symbols up there (Δy/Δx) reflect the core of what derivative calculus is concerned with. It’s the study of how fast things are changing. Δy is, conventionally, the change in the vertical-axis value, whereas Δx is the change in the horizontal-axis value. If you remember your geometry, you might recall that the slope of a line is “rise over run,” or “how much does the line go up or down in a given horizontal space?” Rise over run IS Δy/Δx. Derivative calculus is nothing more exotic than finding the slopes of lines, but the algebra does get a bit hairy because of people wanting to get the slopes of lines that are tangent to single, instantaneous points on a curve YOUR EYES ARE GLAZING OVER, I KNOW.
Let’s un-abstractify this. (Un-abstractify is totally a word. I just created it. Send me royalties.)
Remember that article I wrote about the importance of transients? Transients are where a change in volume is high, relative to the amount of time that passes. An uncompressed snare-drum note has a big peak that happens quickly. It’s the same for a kick-drum hit. The “thump” or “crack” happens fast, and decays in a hurry. The difference in sound-pressure from “silence” to the peak volume of the note is Δy, and the time that passes is Δx. Think about it – you’ve seen a waveform in an audio-editor, right? The waveform is a graph of audio intensity over time. The vertical axis (y) is the measure of how loud things are, and the horizontal axis (x) is how much time has passed. Like this:
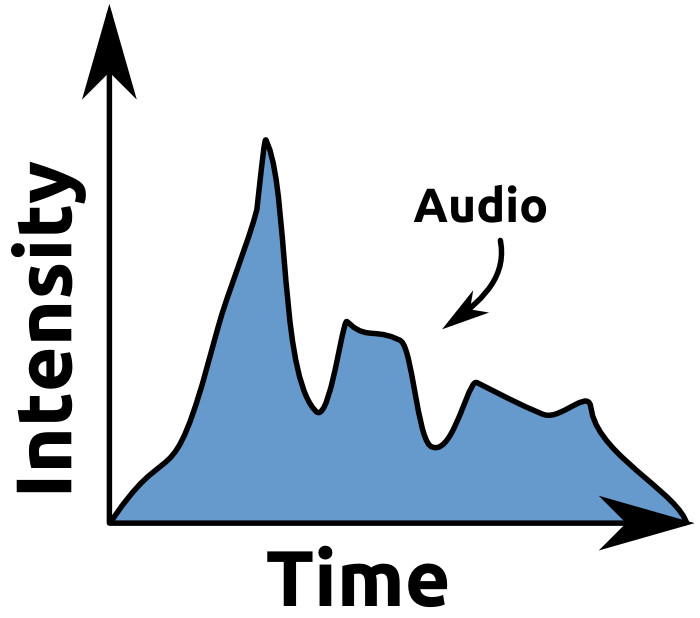 Want to use this image for something else? Great! Click it for the link to a high-res or resolution-independent version.
Want to use this image for something else? Great! Click it for the link to a high-res or resolution-independent version.For music to be really exciting, there has to be dramatic change. For music to be calming, the change has to be restrained. If you want something that’s danceable, or if you want something that has defined, powerful impact regardless of danceability, you’ve got to have room for “big Δy.” There has to be space for volume curves that have steep slopes. The derivative calculus has to be interesting, or all you’ll end up with is a steady-state drone (or crushingly deafening roar, depending on volume) that doesn’t take the audience on much of a ride. (Again, if you want a calming effect, then steady-state at low-volume is probably what you want.) This works across all kinds of timescales, by the way. Your music might not have sharp, high-speed transients that take place over a few milliseconds, but you can still move the audience with swells and decrescendos that develop over the span of minutes.
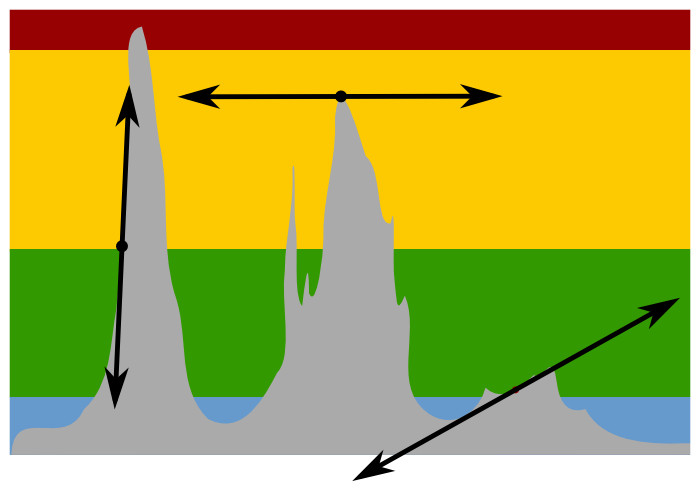
Oh, and that graphic at the top of the page? That’s actually a roughly-traced vocal waveform, with some tangent-lines drawn in to show the estimated derivatives at those points. The time represented is relatively small – about one second. Notice the separation between the “hills?” Notice how steep the hills are? It turns out that the vocal in that recording is highly intelligible, and I would strongly argue that a key component in that intelligibility is a high rate of change in the right places. Sharp transitions from sound to sound help to tell you where words begin and end. When it all runs together, what you’ve got is incoherent mumbling. (This even works for text. You can read this, because the whitespace between words creates sharp transitions from word to word. This,ontheotherhand…)
Oh, and from a technical standpoint, headroom is really important for delivering large “Δy” events. If the PA is running at close to full tilt, there’s no room to shove a pronounced peak through it all. If you want to reproduce sonic events involving large derivatives, you have to have a pretty healthy helping of unused power at your disposal.
Now, overall level does matter as well, which leads us into another aspect of calculus.
Integral Volume
Integral calculus contrasts with derivative calculus, in that integration’s concern is with how much area is under the curve. From the perspective of an audio-human, the integral of the “sonic-events curve” tells you a lot about how much power you’re really delivering to those loudspeaker voice-coils. Short peaks don’t do much in terms of heating up coil windings, so loudspeakers can tolerate rather high levels over the short term. Long-term power handling is much lower, because that’s where you can get things hot enough to melt.
From a performance perspective, integration has a lot to say about just how loud your show is perceived to be. I’ve been in the presence of bands that had tremendous “derivative calculus” punching power, and yet they didn’t overwhelm the audience with volume. It was all because the total area under the volume curve was well managed. The long-term level of the band was actually fairly low, which meant that people didn’t feel abused by the band’s sound.
This overall concept (which includes the whole discussion of derivatives) is a pretty touchy subject in live audio. That is, it can all be challenging to get right. It’s situationally dependent, and it has to be “just so.” Too much is a problem, and too little is a problem. For example, take this blank graph which represents a hypothetical, bar-like venue where the band hasn’t started yet:
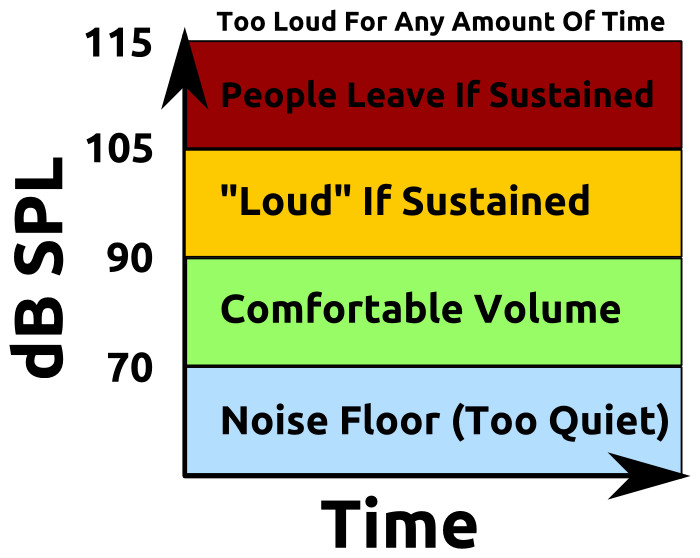 Want to use this image for something else? Great! Click it for the link to a high-res or resolution-independent version.
Want to use this image for something else? Great! Click it for the link to a high-res or resolution-independent version.If the band volume’s area under the curve is too small, they’ll be drowned out by the talking of the crowd. Go too high, though, and the crowd will bail out. It’s a balancing act, and one that isn’t easy to directly define with raw numbers. For instance, here’s an example of what (I think) some reggae bands might look like over the span of several seconds:
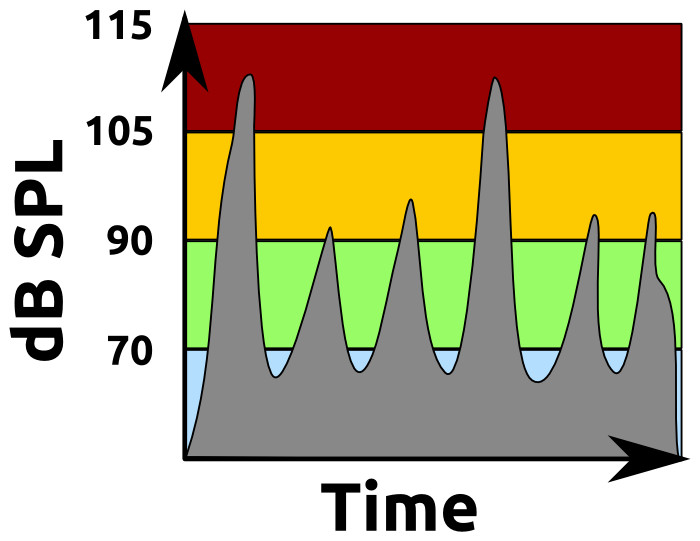 Want to use this image for something else? Great! Click it for the link to a high-res or resolution-independent version.
Want to use this image for something else? Great! Click it for the link to a high-res or resolution-independent version.The “large Δy” events reach deep into the really-loud zone, but they’re very brief. Further, there are places where the noise floor peeks through significantly. This ability for the crowd to hear themselves talking helps to send the message that the band isn’t too loud. Overall, the area under the curve is probably halfway to three-quarters into the “comfortable volume” zone. Now, what about a “guitar” band:
 Want to use this image for something else? Great! Click it for the link to a high-res or resolution-independent version.
Want to use this image for something else? Great! Click it for the link to a high-res or resolution-independent version.The peaks don’t go up quite as far. In terms of sustained level, the band is probably also halfway to three-quarters into the comfortable zone – and yet some folks will feel like the band is a bit loud. It’s because the sustained roar of the guitars (and everything else) is enough to completely overwhelm the noise floor. The crowd can’t hear themselves talk, which sends the message that the band’s intensity is higher than it is in terms of “pure numbers.”
As an aside, this says a lot about the problems of the volume war. At some point, we started crushing all the exciting, flavorful, “large Δy” material in order to get maximum area under the curve…and eventually, we started to notice just how ridiculous things were sounding.
And then there’s one of my pet peeves, which is the indie-rock idiom of scrubbing away at a single-coil-pickup guitar’s strings with the amp’s tone controls set for “maximum clang.” It creates one of the most sustained, abrasive, yet otherwise boring noises that a person can have the displeasure of hearing. Let me tell you how I really feel…
Anyway.
Excitement, intelligibility, and appropriate volume levels are probably just a few of the things described by the calculus of music. I’ll bet there’s more out there to be discovered. We just have to keep our cross-disciplinary antennae extended.