Comb filtering. The weird, hollow sound. The heart of the flanger’s “747 flying overhead” effect. The annoying airhose-esque noise.

What is it? Where does it come from? Why does it behave like it does?

Phase

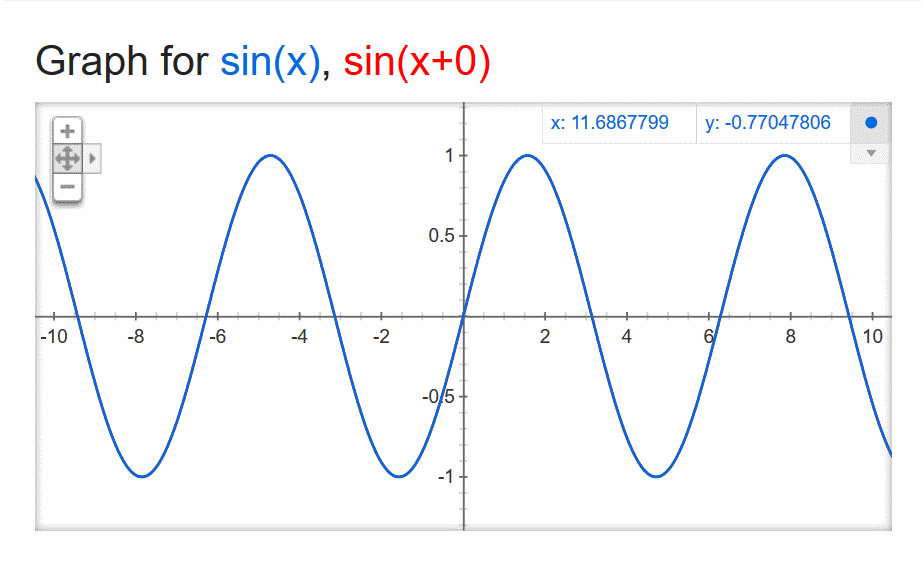
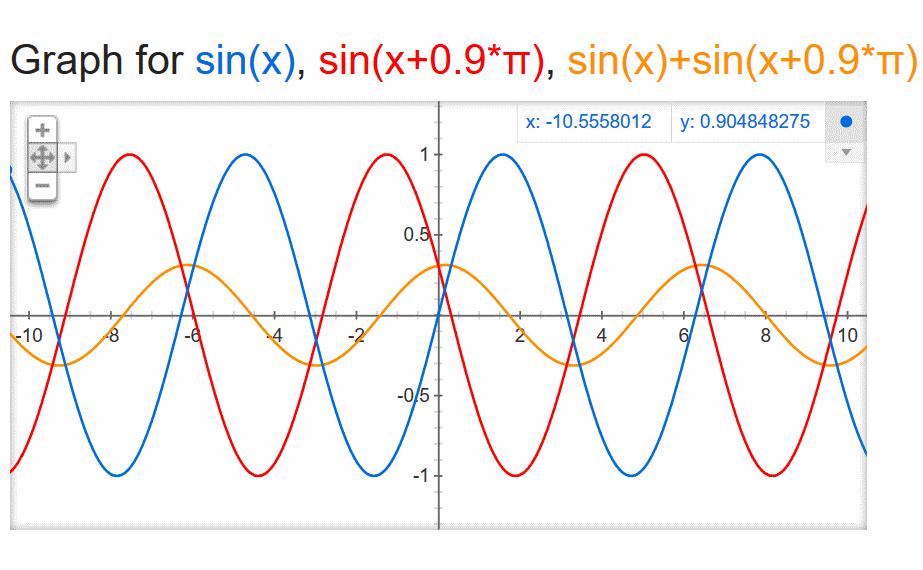
The heart of comb filtering is phase – that is, a time-arrival difference between two sonic events of the same frequency. For instance, here are two events (at an arbitrary frequency) that have no time difference at all. Don’t worry about all the symbols and numbers, just look at the lines on the graph.

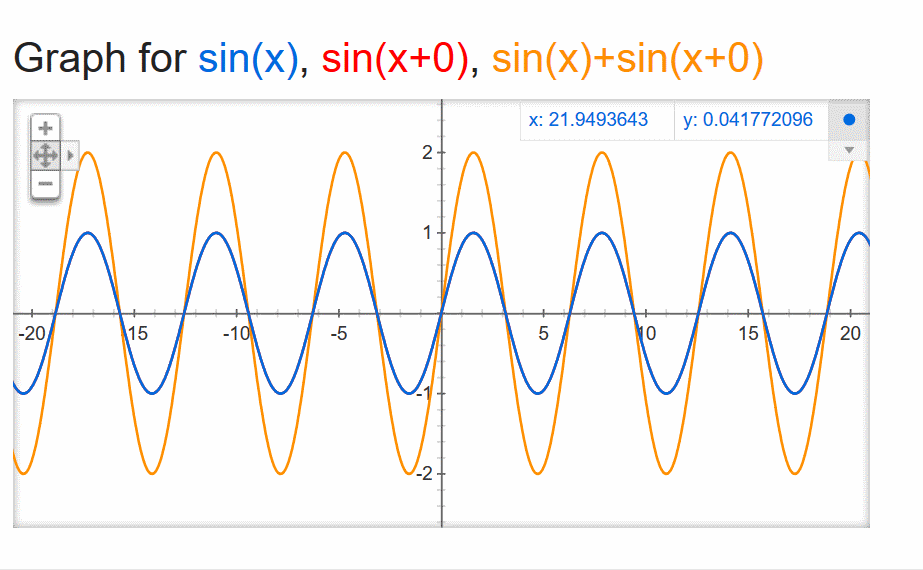
If these events are mathematically combined, they constructively interfere, like this (the orange trace):

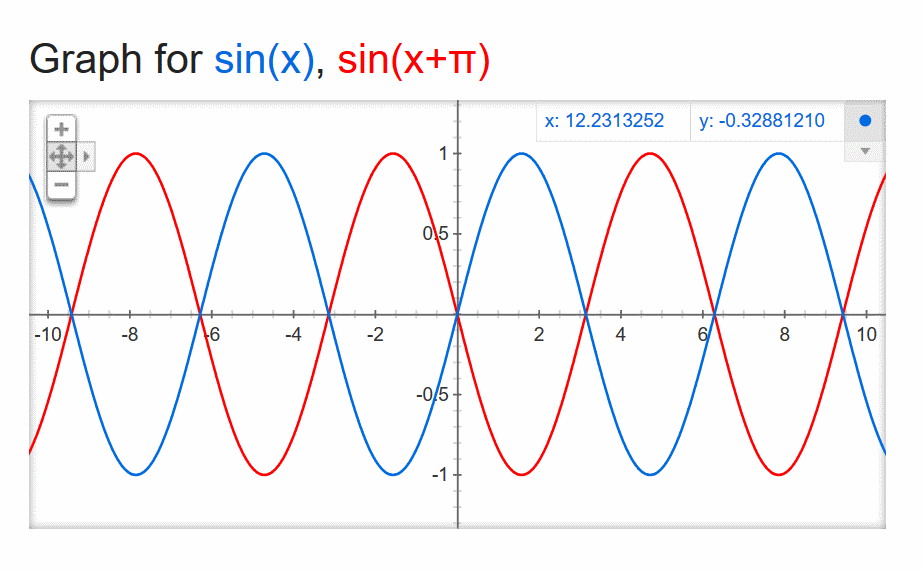
Now, let’s make one of the events “late” when compared to the other. Specifically, let’s make it late enough that it’s completely out of phase. When one event’s amplitude is positive, the other event’s amplitude is the precise negative. This is a phase difference of 1/2 cycle, or 180 degrees.

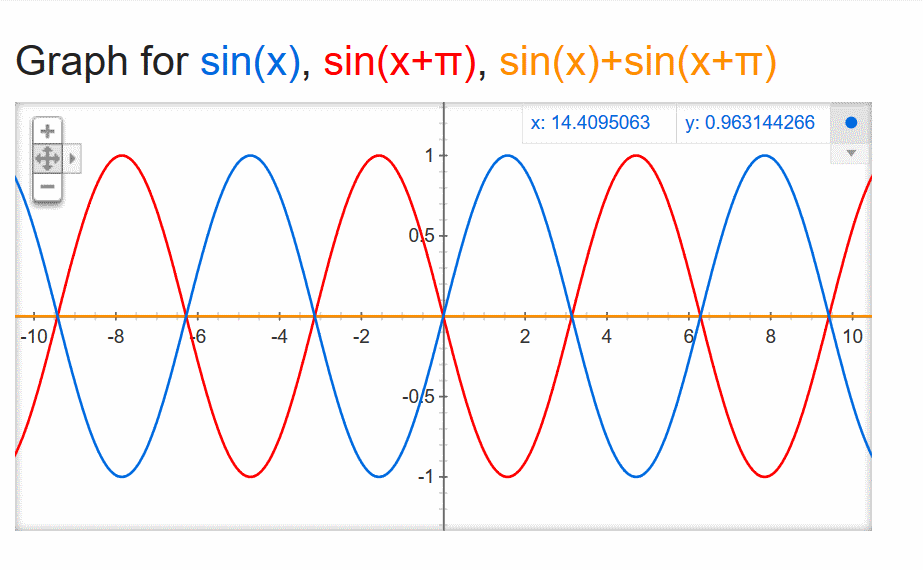
If those two events are combined, say, by arriving at a listener’s ear canal, or via a summing operation in a console, you get cancellation at the frequency in question:

If the delay is reduced, then the cancellation isn’t complete.

More Content

Now then.

Let’s say that the example above was a 1 kHz tone. A wave with a frequency of 1 kHz requires 1 ms to complete a full cycle. A half cycle, then, is half the time, or 0.5 ms. If you take two 1 kHz signals, delay one 0.5 ms, and then combine them, the output signal should be silence. The signal that’s a half cycle late is fully negative when the undelayed signal is fully positive.

Now, let’s imagine a different set of signals. Each signal contains three, pure tones: 1, 2, and 3 kHz. As before, 1 kHz has a period (a cycle time) of 1 ms, whereas the 2 kHz wave cycles twice as fast, and 3 kHz cycles three times as fast. Let’s delay one signal 0.5 ms again.

What happens is that the delayed signal is late by a different number of cycles at each frequency.

1 kHz : 0.5 ms/delay * 1 cycles/ms = 0.5 cycles.
2 kHz : 0.5 ms/delay * 2 cycles/ms = 1 cycle.
3 kHz : 0.5 ms/delay * 3 cycles/ms = 1.5 cycles.

The 1 kHz tone cancels, as we would expect. The 2 kHz wave does NOT cancel. Because the delay is one full cycle, the effect is constructive addition – after the first 0.5 ms has passed, of course. Where things get very interesting is at 3 kHz, because that’s where another cancellation occurs. The 3 kHz tone’s amplitude goes one full cycle, and then only gets halfway when its delayed version begins. Because 3 kHz is at a halfway point when its delayed version starts, the 3 kHz tone also cancels.

You can begin to imagine what would happen if the two signals had content all the way up through the end of the audible spectrum. The phase difference would continue to “wrap” from all the way out of phase to “in phase, but late,” and back again.

Locating The Dips

An important note:

For these examples, I’m working in an electronic system where wavelength doesn’t matter. In a real room, with sound pressure waves in air, the numbers get to be a bit different. Sound travels at about 1126 feet/ second in the air, so a 1 kHz wave is physically 1.126 feet long. For sounds that are physically combining in air, the actual wavelength “in the room,” and the delay time corresponding to that are what determine where comb filtering occurs.

At the same time, rounding things off so that 1 ms = 1 foot will get you into the ballpark, and make math easier. Just be aware that the rounding error is occurring.

---

Comb filtering can occur in all manner of “same signal, but late” situations. One common situation is two microphones picking up the same sound, at a similar amplitude, but with some spacing between the mics.

Let’s assume that our two mics are 2 feet apart. We’ll use the 1 ms = 1 foot rounding to keep the math easy, recognizing that the numbers won’t be exact. A sound arrives at one mic, and then travels onward to the other. The mics are then summed in the console to feed the PA.

For any given delay time, there is a lowest frequency of complete cancellation. This is the frequency which has a cycle time that is twice the delay. At that frequency, one delay time is half a cycle. Frequencies lower than the first cancellation will all be somewhat out of phase, of course, but to lesser degrees.

In more practical terms, this means that (1/[delay in seconds])/2 will give you the frequency with the first complete cancellation. For the above example this works out to (1/[0.002])/2 = 250 Hz.

Above the first cancellation, the cancellation repeats as the phase relationship “wraps” from fully out of phase, to late but in phase, and back again.

These cancellations occur at each odd-numbered harmonic of the first cancellation frequency. Each odd-numbered harmonic is a frequency that is some number of cycles + 1/2 cycle at the delay time.

For our example, this means:

First cancellation – 250 Hz.
Other cancellations – 750 Hz, 1250 Hz, 1750 Hz, 2250 Hz, 2750 Hz, 3250 Hz, 3750 Hz, and so on.

Below is a calculator to help you. It takes a delay time in milliseconds, finds the first cancellation, and then finds the upper cancellations through the audible frequency range.