The world of live audio has many frustrating moments wrapped inside it, but very few of those moments is as frustrating as when the cargo vehicle refuses to wrap enough gear inside of itself. If you haven’t come to the end of your cargo space with one more box left to go inside, you may not actually have done this job.

Those of us who have spent a significant time either generating or augmenting musical noises will, generally, have gotten an intuitive grasp of “truck packing.” It’s basically 3D Tetris. You try to find nooks and crannies that might fit your gear, and then you rotate and relocate that gear to wedge into the hole you found. This process is repeated until you run out of gear to pack, or you run out of room (at 1 AM, with snow falling, a flood of tears welling up in your eyes, and a growing urge to sit down with an alcoholic beverage so as to re-examine your life).

Sometimes you run out of room because you simply have too much gear for the truck, van, SUV, moose-powered sleigh, or jet-equipped platypus. At other times, though, you get stymied due to bad math. Packing is applied geometry, and geometry, like all regular math, runs on a system of predictable rules.

The key rule to getting the most out of your cargo space can’t be talked about until we establish the meta-rule, however:

All cargo-packing must be done in a way that allows the cargo vehicle to be operated safely. If a mathematically perfect pack prevents the vehicle from being operated safely, the pack must be changed.

So, there’s the meta-rule. Here’s the key bit of math, assuming that you start with the largest items first (they have the least flexibility in terms of finding a space to squeeze into):

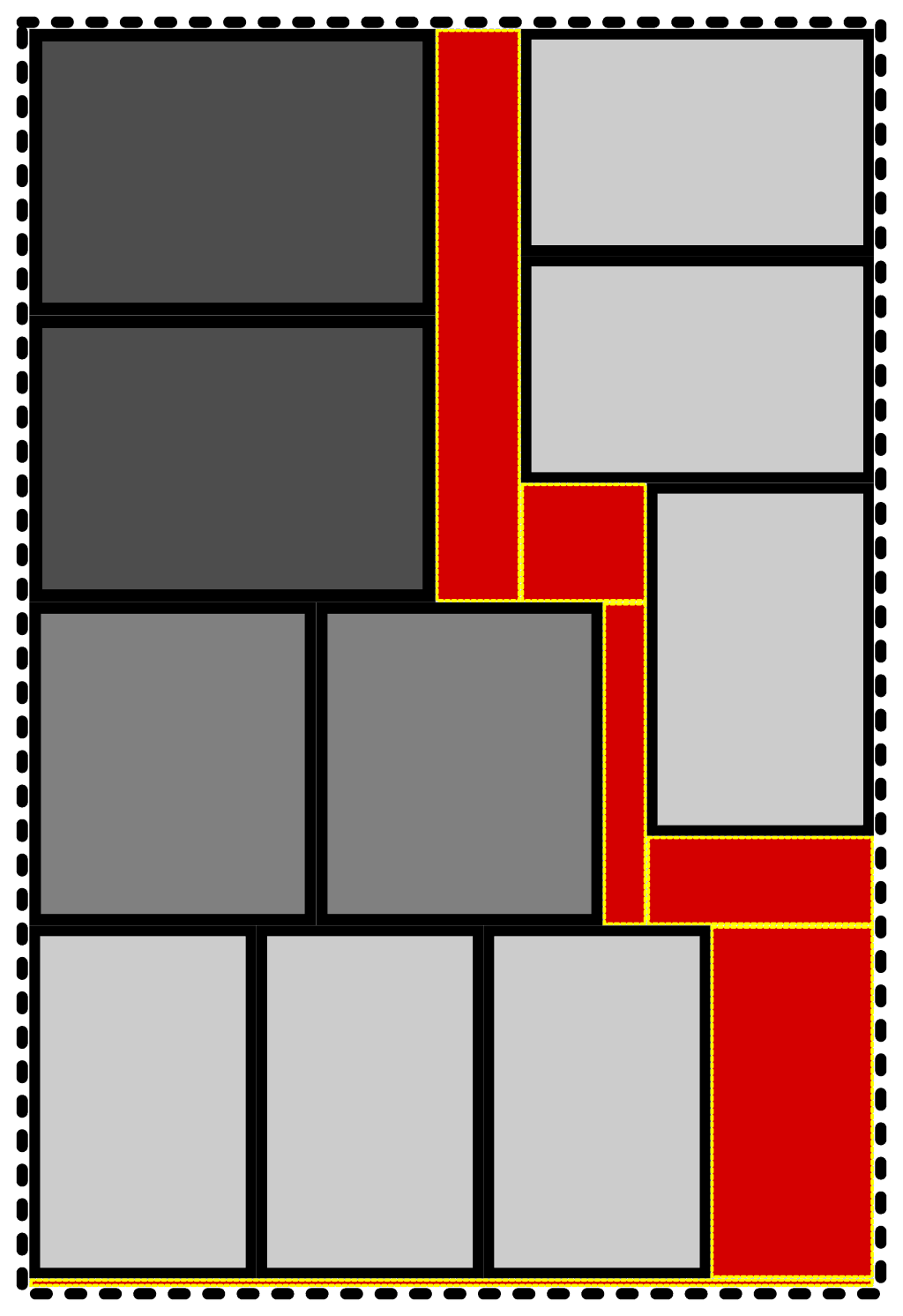
At any point in the pack, the remaining cargo space can be subdivided into one more more volumes described by a rectangular prism (a cubic or rectangular box). Each imaginary box of remaining space should be as large as possible; The number of imaginary boxes should be as few as possible.

In real life, this is a 3D problem. However, to make it easier to visualize, I’ll show some 2D examples. Below is our 2D cargo vehicle, with 2D roadcases strewn all around. If we can arrange the cases such that they are inside the dotted outline of our cargo vehicle, we can get to the gig.

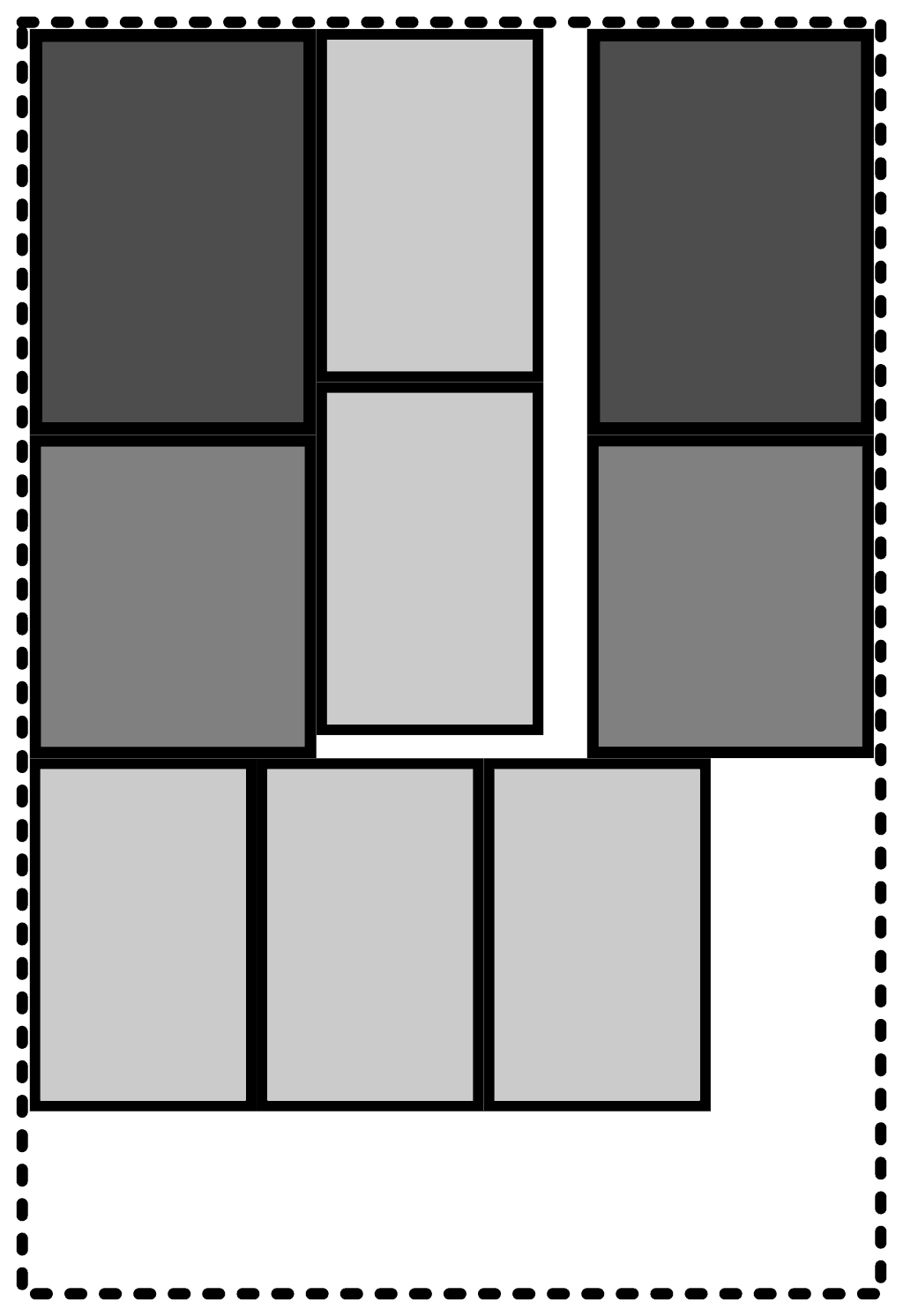
Our first try doesn’t go so well. There are supposed to be six of those light grey boxes, but we only got five in the van. The pack looks very efficient and orderly, but it doesn’t work.

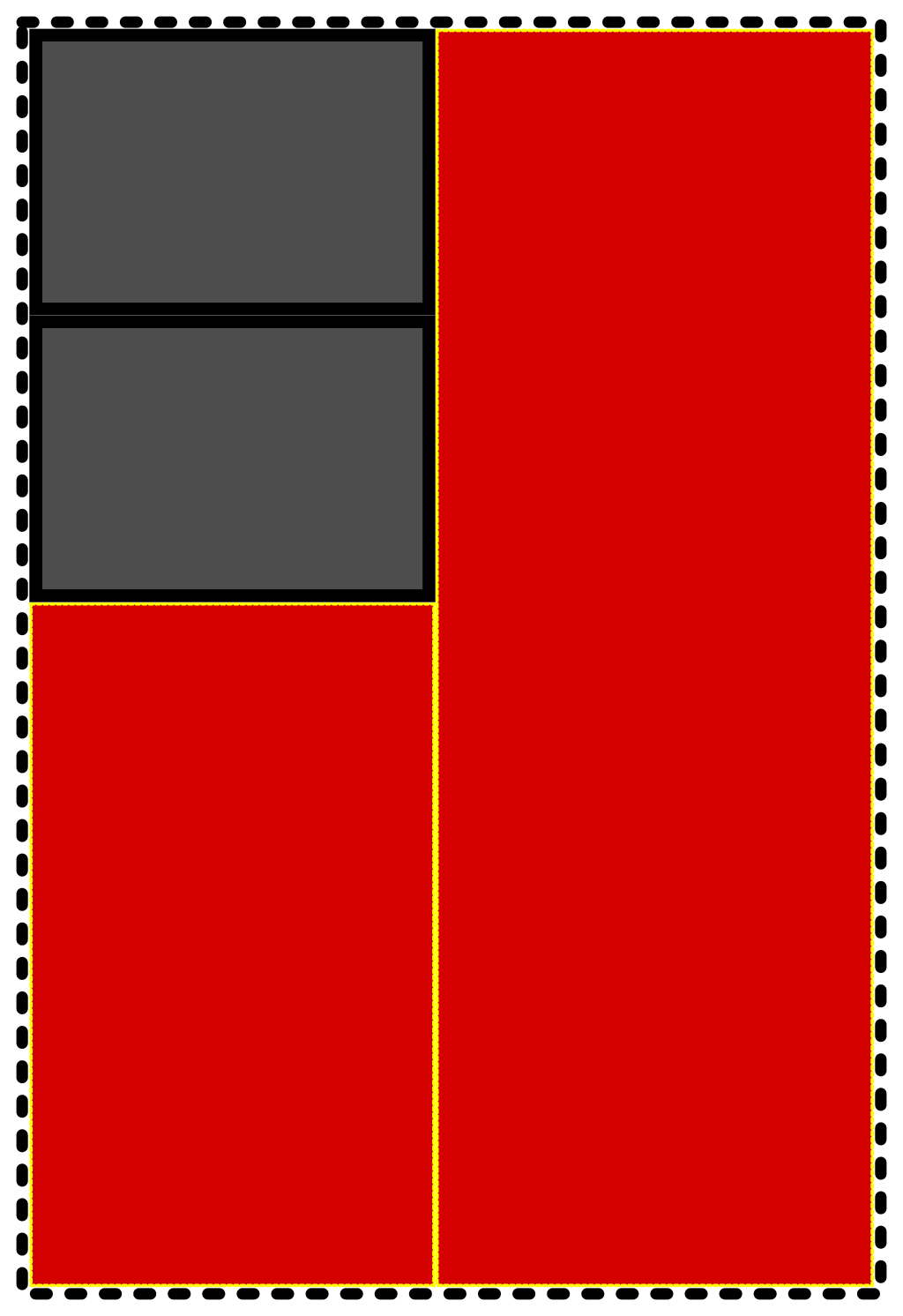
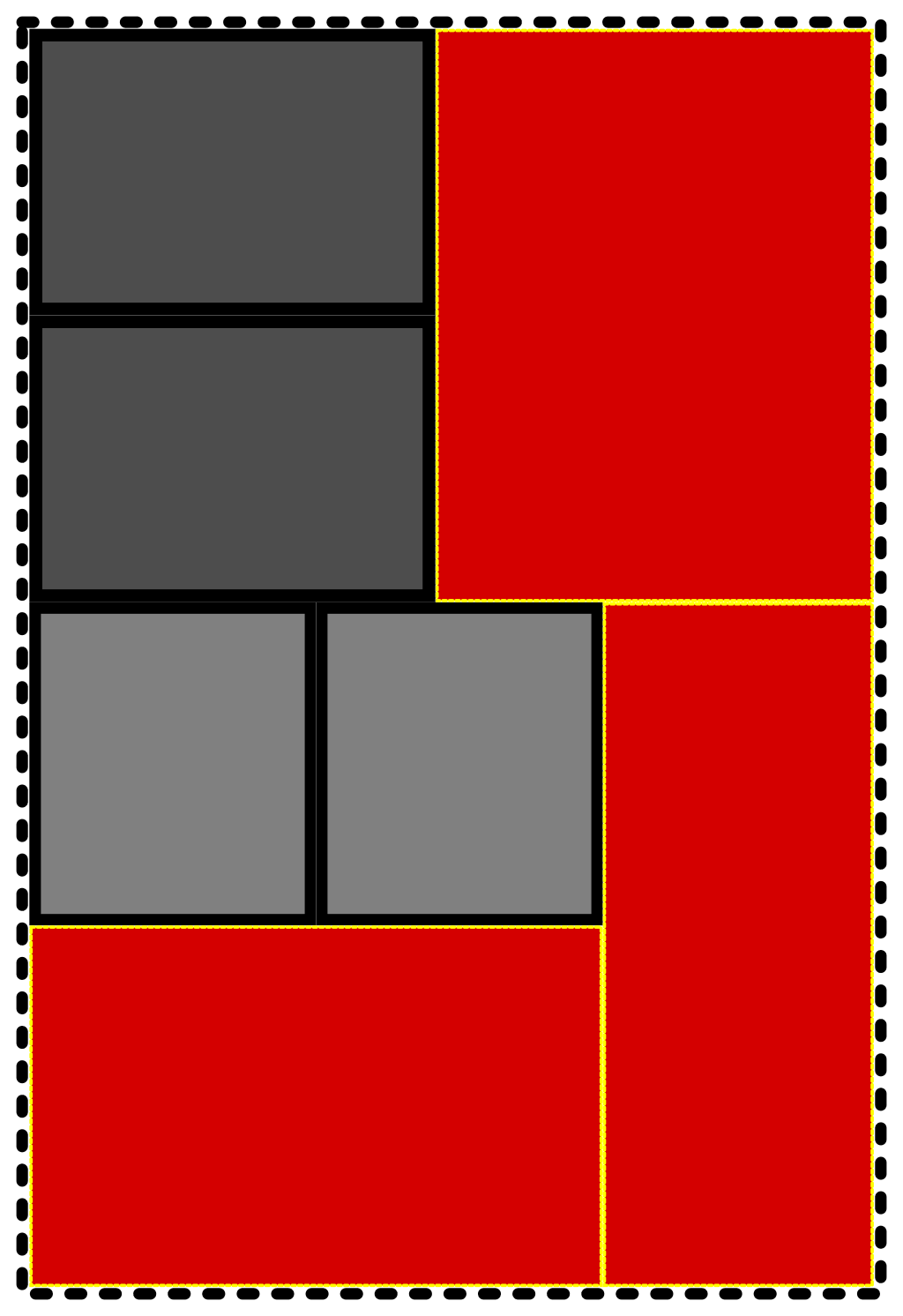
But, if we’re careful about continually maximizing the remaining, contiguous space during the pack, we actually make it. It’s important to note that concessions have to be made for other, physical practicalities, like generally being able to load the vehicle from the front to the back.

The end result doesn’t look as orderly as our first try, but it actually lets us transport all the necessary boxes.